こんにちは。
今日は「フォンミーゼス・フィッシャー分布 ( von Mises-Fisher distribution)」について調べたのでそのことについてまとめます。PRMLの2章にも出てくる分布です(2章はこの前勉強会で話したんですがしんどかったです)。
◯フォンミーゼス・フィッシャー分布(Von Mises–Fisher distribution)とは
この確率分布が出てくると必ずみかけるのがこの図です(笑)。
フォンミーゼス・フィッシャー分布は、簡単に言うと「方向データに対する確率分布」です。方向データ、すなわち球面上における確率分布と考えれば、このような図がでてくるのもなるほどとなりますし、平均の方向ベクトルと同じ方向のベクトルであれば、大きな値になるのかなぁとかっていうのも想像できます。
といっても、まったくわかりませんよね笑(私がそうでした)。そこらへん解説していきます。
■方向データ(周期変数)とは
方向データとは、その名の通り「方向にだけ意味があるデータ」です。例えば円周上にのみ存在するデータ集合みたいな感じでしょうか。
ちゃんと定義してやると、$d$ 次元におけるデータ集合、$ \mathbf{D} = \{ \mathbf{x}^{(1)}, ..., \mathbf{x}^{(n)} \} $ なデータが与えられているときに、任意の $n$ について、$ \mathbf{x}^{(n)^{T}} \mathbf{x}^{(n)}$ が成り立つデータ集合全体のことを指します。
まぁつまり、データの大きさには意味を持たず、とにかく円周上や球面上のどこにあるか、すなわち角度にのみ意味を持つデータ集合って感じです。
角度にのみ意味を持つといえば、周期変数(ある一定周期で同じところに戻ってくる変数)です。これは24時間ごととか、2πごととか、そういう周期ごとの値です。
■余談:ガウス分布の周期変数への一般化としてのフォンミーゼス・フィッシャー分布
確率分布としては代表的なガウス分布をこういった方向データや周期変数に対してそのまま適用するみたいなことはできません。そこで、ガウス分布を周期変数へ一般化させた例として、今回説明しているフォンミーゼス・フィッシャー分布があります。
これについては、PRMLの2.3.8に解説がありますので、見たい方はそちらをどうぞ。
やっていることとしては、周期変数をパラメーター $\theta$ を導入して表現し、そのパラメーターを用いて $cos$ や $sin$ を用いて正規分布を書き換えていくということをしてフォンミーゼス・フィッシャー分布を導出し、それに対して最尤推定を行っているだけなので、普通に数式を追えばわからないことはないと思います(めんどくさいですが)。
■フォンミーゼス・フィッシャー分布の定義
さて、定義ですが、いろんな表現方法ができるので、いろんな定義で書かれていますが、以下では一つだけ示します(異常検知と変化検知の本を読んでいるときに勉強しなおしたので、その本の定義を参考にしています)。
フォンミーゼス・フィッシャー分布では、次の2つのパラメーターを持ちます。
- 平均方向: $\mathbf{\mu}$
- 集中度: $\kappa$
わかりやすさのため、円周上の方向データをイメージします。平均方向とは、文字通り平均値です。集中度は、分散の逆数である精度ととらえるとわかりやすいです。
集中度の値が小さいと、値が円周上全体に広がっていて、集中度の値が大きいと、平均方向の近くにデータが集中していることになります。これについては後でPythonで試してみた例を示すので、それの方がわかりやすいと思います。
この二つのパラメーターを用いて、次のように定義されます。
$$
M( \mathbf{x} | \mathbf{\mu}, \kappa) = \frac{ \kappa^{M/2 - 1} }{ (2\pi)^{M/2} I_{M/2 - 1} ( \kappa ) } \exp (\kappa \mathbf{ \mu }^T \mathbf{x} )
$$
ここで、 $I_{M/2 - 1} ( \kappa )$ は、以下で定義される第1種ベッセル関数です。
$$
I_{\alpha} ( \kappa ) = \frac{ 2^{ -\alpha } \kappa^{ \alpha }}{ \sqrt{ \pi } \gamma ( \alpha + (1/2)) } \int_0^{\pi} \d \phi \sin^{2 \alpha} \phi e^{\kappa \cos \phi}
$$
○Pythonで分布を確かめてみる
pythonで愚直に書いてみました。以下がコードです。
%matplotlib inline import numpy as np import matplotlib.pyplot as plt import seaborn as sns from scipy.special import iv def von_mises_fisher_dist(x, mu, k): # normalize parameter def C(M, k): return k ** (M / 2 - 1) / \ ((2 * np.pi) ** M / 2 * iv(M / 2. - 1, k)) return C(x.ndim, k) * np.exp(k * np.dot(mu, x)) def normalize(x, axis=1): l2 = np.linalg.norm(x, axis=axis, keepdims=True) return x / l2 def __main(): # parameters N = 1000 M = 10 k = 0.1 # set data x = np.random.random([N, M]) x = normalize(x) mu = normalize(x.mean(axis=0), axis=0) # visualization dist = [von_mises_fisher_dist(i, mu, k) for i in x] sns.distplot(dist, kde=False) plt.title("von Mises-Fisher distribution | k = {}".format(k)) plt.xlabel("pdf") plt.ylabel("Freq") plt.show() if __name__ == "__main__": __main()
上のコードの集中度パラメーターである $k$ をいじって、いろんな図を表示させると値のばらつきの変化がわかります。
■ $k=0.1$

■ $k=0.5$
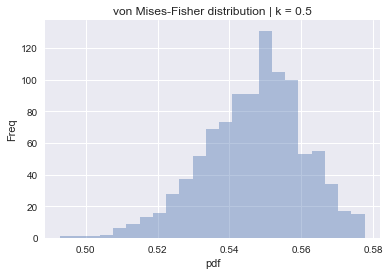
■ $k=10$

◯最尤推定
最尤推定してみます。データ集合 $\mathbf{D}$ から求めるべきパラメーターは、先ほども登場した以下の2つのパラメーターです。
- 平均方向: $\mathbf{\mu}$
- 集中度: $\kappa$
しかし、集中度の方は、ベッセル関数の中にも入り込んでいるので、解析的には解けません。なので、ここでは平均方向のものだけ求めてみます。
実装でも出てきていますが、簡単のために分布の係数を $C_M (\kappa)$ とおきます。尤度関数は、以下のように書くことができ、
$$
L (\mathbf{mu}, \kappa | \mathbf{D}) = \ln \prod_{ n=1 }^{N} C_M (\kappa) e^{\kappa \mathbf{\mu}^T \mathbf{x}^{(n)}} = \sum_{n=1}^{N} \{ \ln C_M (\kappa) + \kappa \mathbf{\mu}^T \mathbf{x}^{(n)} \}
$$
$\mathbf{\mu}^T \mathbf{\mu} = 1$ をラグランジュ係数 $\lambda$ を使って取り込んで、その式を $\mathbf{\mu}$ に関して微分して計算し、$\mathbf{\mu}^T \mathbf{\mu} = 1$ と連立させると、以下のような解を得ます。
$$
\hat{ \mathbf{ \mu } } = \frac{ \mathbf{m} }{ \sqrt{ \mathbf{m}^T \mathbf{m} } }
$$
ただし、
$$
\mathbf{ m } = \frac{1}{N} \sum_{n=1}^{N} \mathbf{x}^{(n)}
$$
です。この結果は、普通に標本平均をとってそれを正規化したものと考えられます。いつもの最尤法の「結局それかい」みたいな(妥当な)結果になっています。
こんなもんですかね。それでは。

